Pyraminx Crystal
The Pyraminx Crystal is a dodecahedral puzzle similar to the Rubik's cube and the Megaminx. It is manufactured and sold by Uwe Mèffert in his puzzle shop since 2008.
It is not to be confused with the Pyraminx, which is also invented and sold by Meffert.
Contents |
History
The Pyraminx Crystal was patented in Europe on July 16, 1987. The patent number is DE8707783U.
In late 2007, due to requests by puzzle fans worldwide, Uwe Mèffert began manufacturing the puzzle. The puzzles were first shipped in February 2008. There are two 12-color versions, one with the black body commonly used for the Rubik's Cube and its variations, and one with a white body.
A company named QJ made an illegal copy of this puzzle in 2010 and Meffert's puzzles files a lawsuit against this company, which is currently on its way.
The Pyraminx Crystal ran out of stock fairly quickly, and became a collector's puzzle. In October of 2011, a new set was created with some slight improvements to the quality.
Description
The puzzle consists of a dodecahedron sliced in such a way that the slices meet at the center of each pentagonal face. This cuts the puzzle into 20 corner pieces and 30 edge pieces, with 50 pieces in total.
Each face consists of five corners and five edges. When a face is turned, these pieces and five additional edges move with it. Each corner is shared by 3 faces, and each edge is shared by 2 faces. By alternately rotating adjacent faces, the pieces may be permuted.
The goal of the puzzle is the scramble the colors, and then return it to its original state.
Solutions
The puzzle is essentially a deeper-cut version of the Megaminx, and the same algorithms used for solving the Megaminx's corners may be used to solve the corners on the Pyraminx Crystal. The edge pieces can then be permuted by a simple 4-twist algorithm, R L' R' L, that leaves the corners untouched, in a manner similar to the Pyraminx. This can be applied repeatedly until the edges are solved.
Number of combinations
There are 30 edge pieces with 2 orientations each, and 20 corner pieces with 3 orientations each, giving a maximum of 30!·230·20!·320 possible combinations. However, this limit is not reached because:
- Only even permutations of edges are possible, reducing the possible edge arrangements to 30!/2.
- The orientation of the last edge is determined by the orientation of the other edges, reducing the number of edge orientations to 229.
- Only even permutations of corners are possible, reducing the possible corner arrangements to 20!/2.
- The orientation of the last corner is determined by the orientation of the other corners, reducing the number of corner combinations to 319.
- The orientation of the puzzle does not matter (since there are no fixed face centers to serve as reference points), dividing the final total by 60. There are 60 possible positions and orientations of the first corner, but all of them are equivalent because of the lack of face centers.
This gives a total of 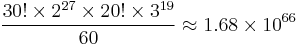 possible combinations.
possible combinations.
The full figure is 167 782 694 255 872 245 204 193 387 189 409 175 281 146 860 685 032 947 712 000 000 000 (roughly 1.68 unvigintillion on the short scale or 1.68 undecillion on the long scale).
See also
References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||